15 resultados
Atividades de Adição para 2º Ano
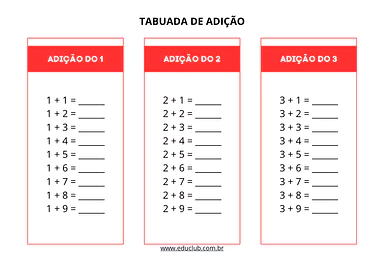
Tabuada de Adição para completar
Para consolidar o aprendizado da adição de forma prática e autônoma, apresentamos a Tabuada de Adição para Completar. Este material é um recurso excelente para que...

Tabuada de adição do 5
Aprender a tabuada do 5 é uma etapa crucial no desenvolvimento aritmético nas primeiras etapas do Ensino Fundamental. A criança aprende a perceber padrões que facilitem...

Tabuada de adição do 4
O estudo da tabuada de adição do 4 auxilia a criança a expandir suas habilidades matemáticas. Observar padrões contribui para o desenvolvimento de estratégias de adição...

Tabuada de adição do 2
A tabuada da adição do 2 leva a criança a dar um passo adiante. Cada operação envolve adicionar 2 a um número dado, o que ajuda...
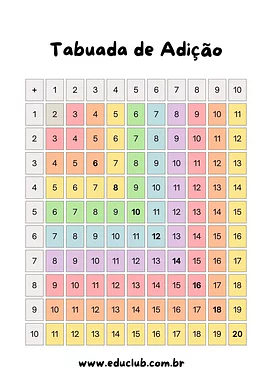
Tabuada de adição completa para imprimir
A adição é uma das primeiras e mais importantes operações que aprendemos na matemática. Ela está presente em nosso dia a dia, desde contar brinquedos até...

Tabuada de adição do 10
A tabuada da adição do 10 traz uma compreensão da prática das somas quando um dos fatores é o 10. Seguir padrões, ajuda as crianças a...

Tabuada de adição do 6
A tabuada da adição do 6 representa um novo desafio para as crianças. Cada vez mais, avançam na adição de números grandes, o que exige a...

Continhas de adição na horizontal para praticar
A atividade Continhas de adição na horizontal para praticar é um recurso didático excelente para consolidar o aprendizado das operações de adição de forma prática e...
Assuntos

Tabuada de adição do 8
A prática contínua com a tabuada de adição do 8 favorece a percepção de padrões nas operações de adição. Isso ajuda a construir a base para...

Tabuada de adição do 7
A tabuada de adição do 7 amplia o conhecimento aritmético das crianças. Cada vez aprendem a dominar a soma de valores maiores, aumentando a confiança na...

Tabuada de adição do 1
A tabuada de adição do 1 é o ponto de partida para trabalhar o cálculo mental. É muito importante, pouco a pouco, desenvolver a prática de...

Tabuada de adição do 9
Tabuada de adição do 9 para que as crianças pratiquem. O uso da tabuada é importante para o entendimento de padrões matemáticos e desenvolvimento de estratégias...

Tabuada de adição do 3
A tabuada de adição do 3 convida a criança a perceber padrões matemáticos quando realiza a soma. Ao praticar a adição do 3, a criança fortalece...
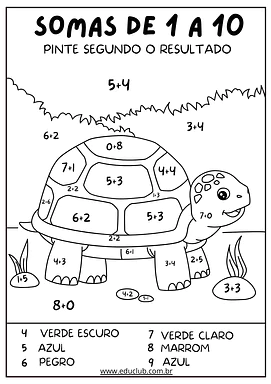
Atividade some e pinte para imprimir
Sabemos que manter as crianças engajadas na prática da matemática pode ser um desafio. Pensando nisso, e como um excelente recurso de apoio ao nosso post...
Assuntos

Atividade de adição do Natal
A Atividade de adição do Natal é um recurso lúdico e eficaz para consolidar o aprendizado da adição, utilizando a temática natalina para engajar os alunos....
Assuntos
A adição é uma das operações fundamentais da matemática, representando a ação de juntar ou acrescentar quantidades. No 2º ano do Ensino Fundamental, o estudo da adição se aprofunda, indo além da simples contagem e introduzindo procedimentos de cálculo mais estruturados.
O que se aprende sobre adição no 2º ano?
Nesta fase, os alunos consolidam os fatos básicos da adição (somas de um dígito) e começam a trabalhar com números de até três ordens (centenas). O principal avanço é a introdução do algoritmo convencional da adição, incluindo o conceito de "reserva" ou "transporte" (o "vai um"), onde a soma de uma ordem (unidade) ultrapassa o valor 9 e precisa ser reagrupada na ordem seguinte (dezena).
Objetivos Gerais
Os objetivos gerais do estudo da adição no 2º ano são:
- Consolidar os fatos básicos: Automatizar as somas mais simples para liberar a memória de trabalho para cálculos mais complexos.
- Compreender o valor posicional: Entender que a posição de um algarismo no número altera seu valor (unidade, dezena, centena) é crucial para realizar os cálculos com reserva.
- Desenvolver o cálculo mental: Utilizar estratégias como a decomposição de números (ex: 25 + 12 = 20 + 10 + 5 + 2) para resolver somas de forma mais ágil. • Resolver problemas: Aplicar o conhecimento da adição para solucionar problemas práticos do cotidiano que envolvam as ideias de juntar e acrescentar quantidades.
Alinhamento com a BNCC
A Base Nacional Comum Curricular (BNCC) orienta o ensino da adição no 2º ano por meio das seguintes habilidades:
- (EF02MA05): Construir fatos básicos da adição e subtração e utilizá-los no cálculo mental ou escrito.
- (EF02MA06): Resolver e elaborar problemas de adição e de subtração, envolvendo números de até três ordens, com os significados de juntar, acrescentar, separar, retirar, utilizando estratégias pessoais ou convencionais.
O foco do estudo da adição no 2º ano do Ensino Fundamental é garantir que o aluno não apenas decore o mecanismo do cálculo, mas que compreenda o processo e saiba aplicá-lo em diferentes contextos, utilizando tanto estratégias pessoais quanto o algoritmo convencional.